Apriori 演算法：頻繁項集與關聯規則方法

摘要

Apriori 演算法是從交易資料中找出項目共現模式的方法，目標是發現哪些項目組合經常同時出現，可再進行推導出具條件性的關聯規則，因此主要兩大目標為找出頻繁項集，以及建立關聯規則。

Apriori 核心概念在於，如果一個集合為頻繁，則任意子集也必定是頻繁項集（Frequent Itemset），整個演算法的主要理論採用 層級搜尋（level-wise search） 也就是通用演算法常見的廣度搜尋方法，所有初始項目集合中將在 項集格（Itemset lattice） 中逐層展開項目集合

Apriori 的基本衡量指標有兩項：

• 支持度（Support）：衡量組合在整體資料中的普遍性

• 可信度（Confidence）：衡量在給定前件時後件發生的可能性

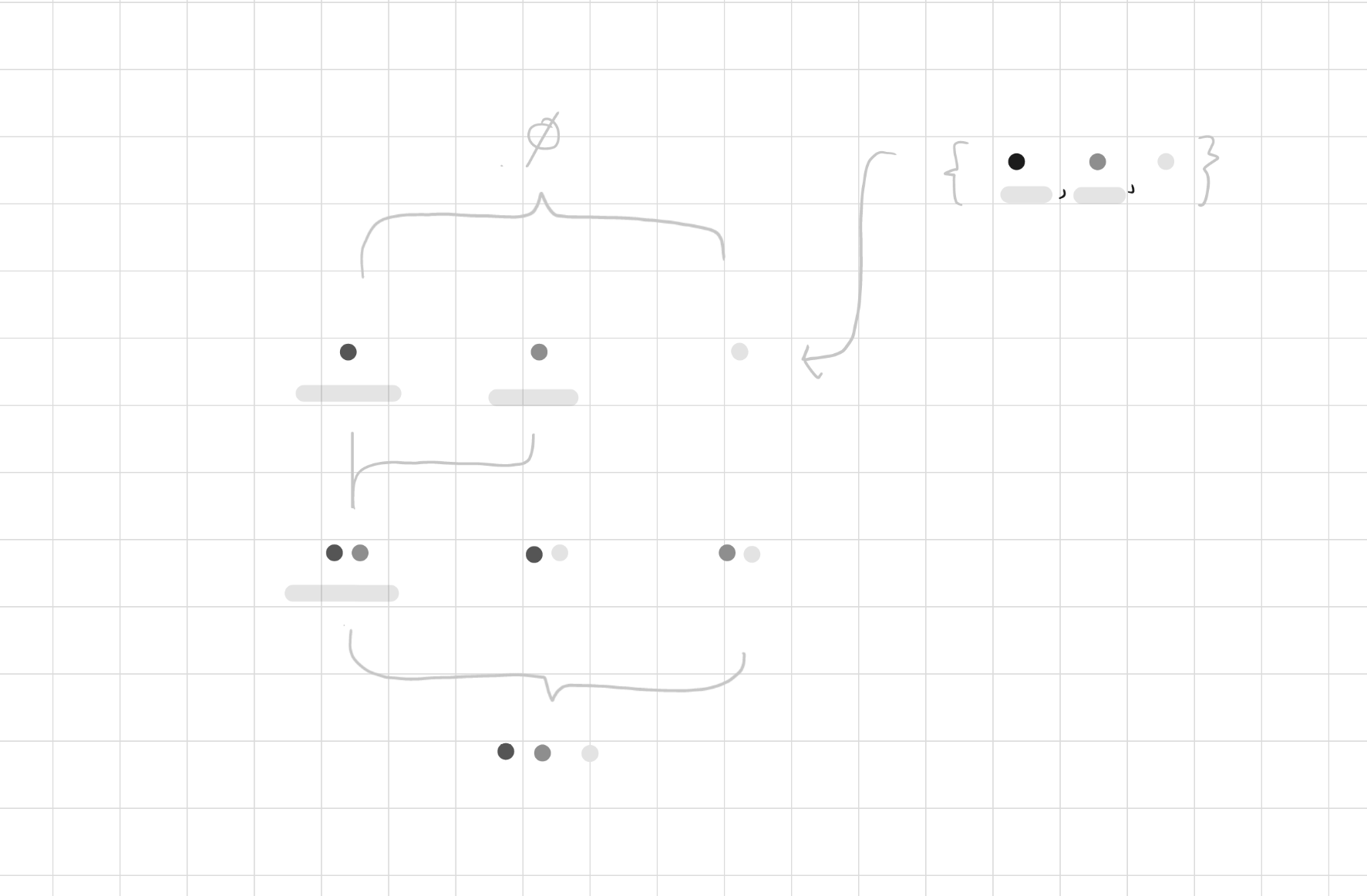
項集格（Itemset Lattice）

項集格理論上將所有排列組合展開，展開過程從單元素項集（1-itemset）開始，逐步生成 k-itemset，而在實際上在低層級時將去除掉非頻繁項集，因此減少了計算空間。

這是一個項目集合所展開所有組合的表示，後續會以k項集（1-itemset）來表示，同時k個項集對應的是樹的層(Level)數

---

Apriori 的整體運作過程

起初輸入所有項目集合，每個集合為一種項目組合

1. 生成候選項集（Candidate itemset）

從交易資料中提取所有單一項目，形成第一層候選項集

2. 計算支持度（Support）

掃描交易資料庫，計算各候選項集的出現頻率，計算方式在所有項目中該項目所出現的次數

$$support(A) = \frac{|A|}{N}$$

3. 篩選頻繁項集（Frequent Itemset）

保留支持度不小於最小支持度門檻的項集，得到頻繁項集，然後該頻繁項集，將提供給下一個層級來作為候選項集

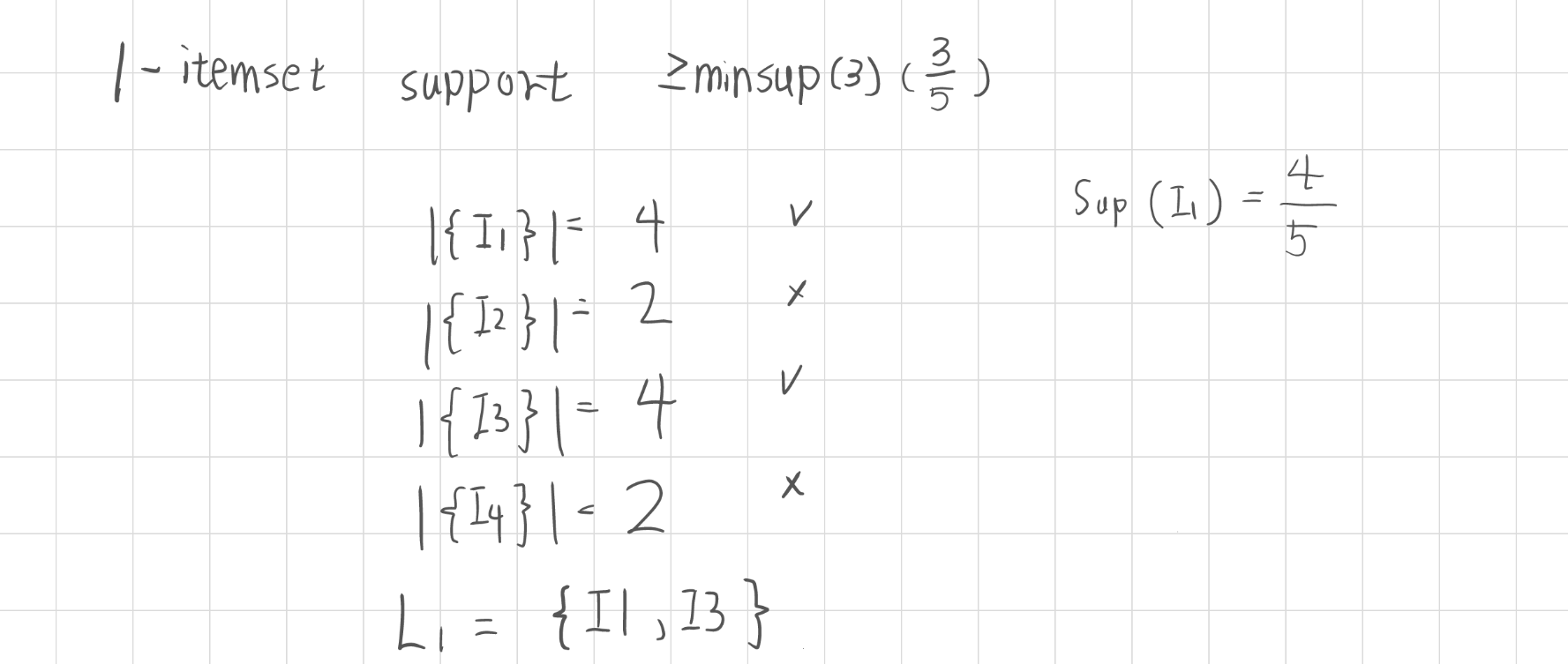
4. 遞迴階段

遞迴至下一個 $k+1$ 項集(k-itemset)，將前面的步驟遞迴，直到無法生成新的候選項集為止

5. 產生關聯規則（Association Rules）

將最終頻繁項集拆解成所有可能的 A → B 規則，並依據可信度（Confidence）門檻 minconfidence 篩選有效規則，衡量該規則在資料中的穩定性與可靠性

$$confidence(A \rightarrow B) = \frac{|A \cap B|}{|A|}$$

可信度（Confidence）實際上為關聯規則的條件機率

使用下圖作為例子，起初需要先計算該集合的支持度，也就是出現頻率，然後在將支持度用於計算可信度，因此如果關聯規為「當獲得 $I_1$ 後在獲得 $I_3$ 的可信度是多少」，則計算為 $\{I_1, I_3\}$ 的支持度除以$I_1$ 支持度