特徵值與特徵向量運算方法(Eigenvalues and Eigenvectors)

第一步是解特徵方程式找到特徵值，第二步是根據特徵值找到對應的特徵向量。

定義

給定一個 $n \times n$ 的方矩陣 $A$，若存在一個非零向量 $X$ 以及一個常數 $\lambda$ ，滿足以下公式

$$AX = \lambda X$$

• $\lambda$ 為矩陣 $A$ 的特徵值（Eigenvalue）
• $X$ 為對應於 $\lambda$ 的特徵向量（Eigenvector）

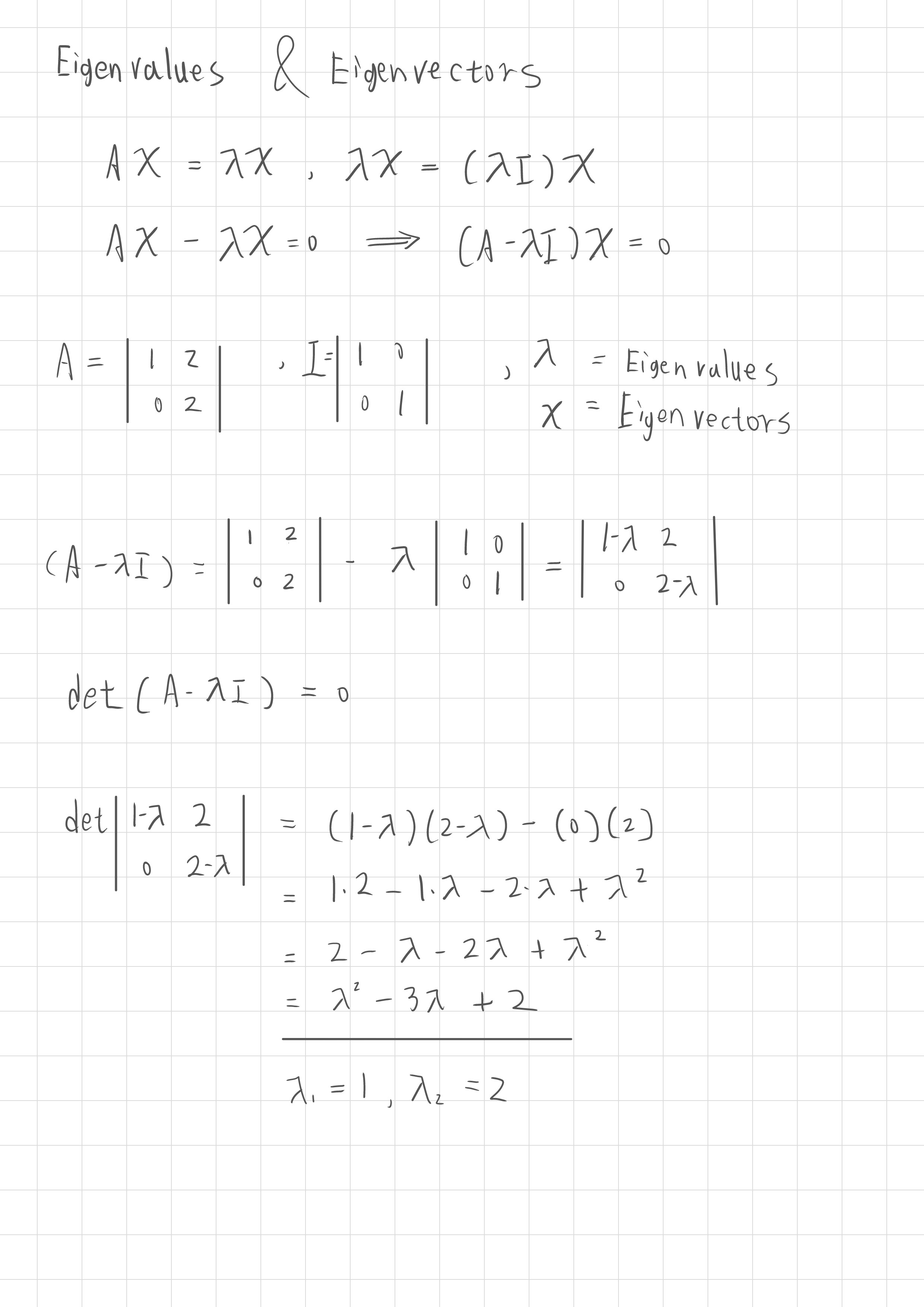
公式轉換

透過對 $\lambda$ 乘上 $I$ 單位矩陣，得到 $\lambda X = (\lambda I) X$，使純量成為特徵矩陣，再透過矩陣乘法的分配律，使$X$合併，得到

$$AX = \lambda X \Rightarrow (A - \lambda I)X = 0$$ $$$$

特徵方程（Characteristic Equation）

只有在 $\det(A - \lambda I) = 0$ 時才會有多個非零解。

$$\det(A - \lambda I) = 0$$

解出特徵值 $\lambda$

這是一個以 $\lambda$ 為變數的多項式方程式，其階數最多為矩陣 $A$ 的階數 $n$，$\lambda$ 的可能解最多有 $n$ 個

求特徵向量 $X$

代入每個 $\lambda$，解該線性系統，找出非零解 $X$。

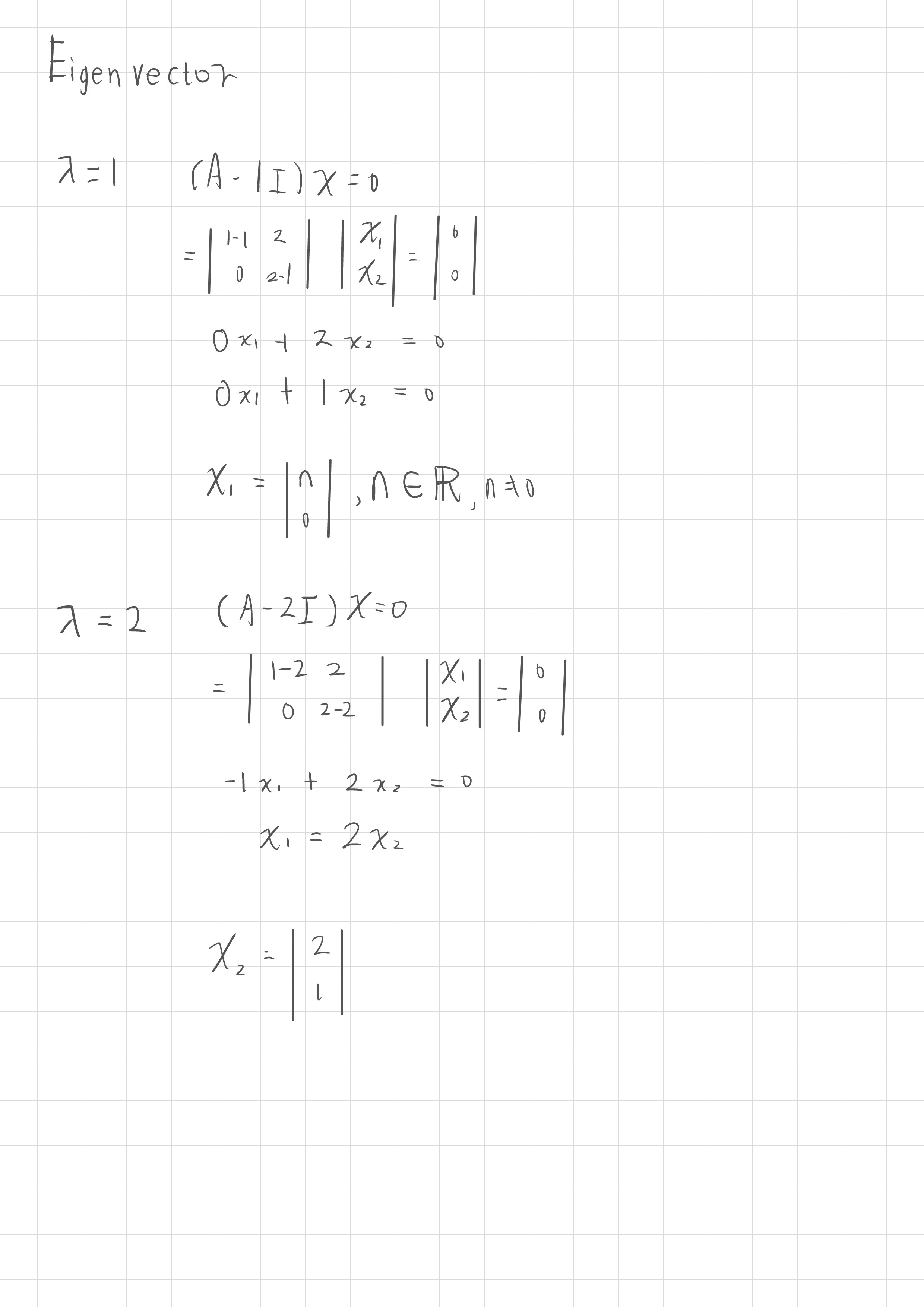
特徵向量用途

以下是的特徵向量用途，聚焦在人工智能領域中，每個部份將在其他文章中探討。

1. 主成分分析（PCA）

利用資料的協方差矩陣的特徵向量進行降維，保留最大變異方向，常用於特徵選擇與視覺化。

2. 奇異值分解（SVD）

將資料矩陣分解為特徵向量與特徵值組合，用於語意分析、推薦系統與資料壓縮。

3. 圖神經網路（GNN）與譜圖理論

透過圖的拉普拉斯矩陣的特徵向量進行節點嵌入與頻譜卷積，實現圖結構學習。

4. 自注意力分析（Self-Attention）

雖非直接依賴特徵向量，但可用特徵值分析理解注意力矩陣的資訊流與結構穩定性。

5. 強化學習（Reinforcement Learning）

轉移機率矩陣的主特徵向量可用來計算穩態策略或長期行為分布。